CP078 – Chuyện vui về phân số
Phỏng theo bài “Fractional Fun” của
“Burkard Polster and Marty Ross”, ngày 27/06/2011
Toán học cổ Ai cập rất đặc sắc về nhiều mặt nào đó, nhưng về những mặt khác thì không đến mức như vậy. Thí dụ như một khía cạnh rất kỳ lạ của toán học cổ Ai cập liên quan với “Phân số”.
Các nhà toán học cổ Ai cập chỉ xét những gì mà chúng ta gọi là “Phân số căn bản”, có tử số bằng 1, thí dụ họ chỉ có khái niệm với 1/5, chớ không với 2/5.
Các phân số căn bản nầy được viết như là số nguyên với dấu chấm hay ký hiệu gì đó ở bên trên. Nhưng để tiện việc theo dỏi, bài nầy vẫn dùng dạng quy ước thông dụng của phân số.
Bằng cách nào các nhà toán học Ai cập giải quyết được bài toán chia 2 cho 5? Họ không thể viết
1/5 + 1/5 vì theo quy ước khi viết tổng số lúc đó, phân số căn bản chỉ được hiện diện một lần!
Thay vì viết 1/5 + 1/5, bài toán chia 2 cho 5 được giải quyết như sau:
Tài liệu cổ Ai cập “ Rhind papyrus” (bản thảo Rhind), niên đại 1800 trước công nguyên, có liệt kê danh sách các các phân số căn bản của các tổng từ 2/5 đến 2/101 có mẫu số là số lẻ. Lẽ dỉ nhiên, các tổng có mẫu số chẳn có thể được đơn giản dễ dàng.
Với 2/7, ta có:
Còn 2/3 thì sao?
Đó là “phân số không căn bản” duy nhất được các nhà toán học cổ Ai cập chấp nhận cho sử dụng với một ký hiệu riêng đặc biệt ! Mặc dầu vậy, người Ai cập vẫn thường dùng dạng phân tích thành phân số căn bản của 2/3 trong các phép tính của họ.
Nhận xét kỹ mẫu số của các dạng phân tích của 2/3, 2/5 và 2/7, ta thấy chúng có một đặc điểm chung là:
3 x 2 => 6, 5 x 3 => 15, 7 x 4 => 28
Áp dụng đặc điểm đó cho các phân số khác, thí dụ 2/9 = 1/5 + 1/45. Kết quả nầy cũng đúng, nhưng không thấy liệt kê ra trong tài liệu “Rhind papyrus”. Trái lại, cách phân tích sau đây được liệt kê:
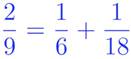
Tại sao vậy? Có lẽ các nhà toán học cổ Ai cập muốn nhanh chóng! chỉ cần chia cho 3 hai vế của dạng phân tích của
2/3 = 1/2 + 1/6 là xong!.
Phương cách đó cũng có thể áp dụng để phân tích nhanh chóng các phân số có mẫu số là bội số của 3, 5, 7, … Tuy nhiên, cách phân tích của các nhà toán học cổ Ai câp rất bất nhất, khi vầy khi khác! Thí dụ: vì 2/5 = 1/3 + 1/15 nên, nếu chia 2 vế cho 7, thì ta có: 2/35 = 1/21 + 1/105. Cách phân tích đó không thấy liệt kê trong bản thảo, trái lại, không biết vì lý do gì, cách phân tích sau đây thì có liệt kê:
Đến đây, độc giả có thể nêu lên câu hỏi:
“Với kiến thức Toán học ngày nay, tìm điều kiện để một phân số có thể phân tích thành tổng số của 2 phân số khác có tử số bằng 1, thí dụ 2 phân số 3/23 và 5/24?”.
Thuận Hoà mời độc giả thử tự mình giải bài toán trên trước khi xem lời giải của Thuận Hoà.
* * *
Cho phân số A/B. Tìm 2 số nguyên và dương x, y sao cho
A/B = (1/x) + (1/y) (1)
Ta có:
(A/B) – (1/x) = (Ax – B) / Bx
Để có (1), ta phải có: Ax – B = 1
==> x = (B + 1) / A (2)
Điều kiện để phương trình (1) có lời giải là:
(B + 1) là 1 bội số của A.
Nếu B + 1 = kA thì x = k theo (2), k là một số nguyên dương.
Từ (1), suy ra:
1/y = (A/B) – (1/k) = (Ak – B) / Bk
hay y = Bk / (Ak – B) (3)
Tóm lại:
Phân số A/B có thể phân tích thành tổng số 1/x + 1/ y khi B + 1 là một bội số của A.
x = k, y = BK / (Ak – B)
k là một số nguyên dương sao cho B + 1 = kA
Áp dụng:
a) Phân số 3/23 => A = 3, B = 23
=> B + 1 = 24 = 8A
=> x = 8 và y = 23×8 / (3×8 – 23) = 184 theo (2) và (3)
=> 3/23 = (1/8) + (1/184)
b) Phân số 5/24 => A = 5, B = 24
=> B + 1 = 25 = 5A
=> x = 5 và y = 24×5 / (5×5 – 24) = 120
=> 5/25 = (1/5) + (1/120)
Chú thích: Cách phân tích trên không phải là duy nhất, như thí dụ sau đây:
2/35 = 1/18 + 1/630 = 1/30 + 1/42
Thuận Hoà
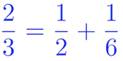
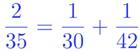
Kỳ BK078 « ĐỌC VUI VÀ SUY NGHĨ said
[…] đọc Chuyện Phiếm mới nhất: Chuyện vui về phân số trong mục Các Tài liệu mới […]