CP085 – Một bài toán mẫu tự đặc biệt
Toán mẫu tự là toán mà những con số từ 0 đến 9 được thay bằng 10 mẫu tự khác nhau trong danh sách mẫu tự từ A đến Z. Trong bài viết nầy, Thuận Hoà xin giới thiệu độc giả một bài toán mẫu tự đặc biệt, có 9 mẫu tự đều khác nhau, đại diện cho 9 con số từ 1 đến 9. Bài toán như sau:
(1)
Câu hỏi của bài toán là:
“Thay thế 9 mẫu tự A, B, C, D, E, M, N, P và Q bằng các con số khác nhau
từ 1 đến 9 sao cho tổng số của 2 phân số AB/CDE và MN/PQ bằng 7.”
Nếu hấp tấp, độc giả có thể cho rằng bài toán quá bất kỳ, không giải được. Làm sao giải được 9 ẩn số mà chỉ có 1 phương trình?
Mời độc giả bỏ vài phút suy nghĩ xem bài toán có gì đặc biệt giúp giải được hay khôngt?
* * *
Để đơn giản, gọi phân số thứ nhất là X, phân số thứ hai là Y => X + Y = 7 (2)
X = AB / CDE => 0 < X < 1 (3)
Để có X + Y = 7 thì 6 < Y < 7 (4)
Tìm được MN và PQ, tức là phân số Y, ta có thể suy ra phân số X:
X = 7 – Y = 7 – (MN/PQ) (5)
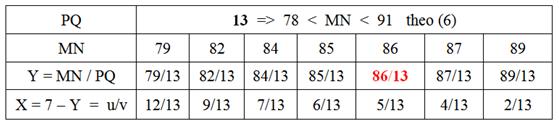
(4) => 6 < MN/PQ < 7 => 6PQ < MN < 7PQ (6)
Nếu PQ ≥ 17 => 6PQ ≥ 102 có 3 con số không thể nhỏ hơn MN có 2 con số.
=> PQ phải lớn hơn 10 và nhỏ hơn 17.
Để ý rằng P khác Q, PQ có thể có các trị số sau đây: PQ = 12, 13, 14, 15, 16
a) Xét trường hợp: PQ = 12 => 72 < MN < 84
Trị số X = u/v trong bảng trên là dạng rút gọn của phân số thứ nhất AB/CDE.
Để có đúng dạng AB/CDE, nhân u và v cho cùng số m sao cho: X = um/vm = AB/CDE
Nếu ta tìm được một số m thoả điều kiện (K) sau đây:
-
10 < um < 100, 100 < vm < 1000
-
Hai tích số um và vm không chứa 0, không chứa các con số trùng nhau và không chứa các con số nào trong PQ và MN
Thì um/vm sẽ có dạng AB/CDE và một đáp số của bài toán sẽ tìm đươc.
Theo bảng trên, v = 12 => vm không thể chứa 1 và 2 => vm = 12m > 300 => m > 25
Với v = 12, vm < 1000 khi m < 84. Với m > 25 và các trị số của u => um >100 => không nhận được, trừ khi u = 1
Với u/v = 1/12 và thay đổi m từ 26 đến 83 , ta không tìm được trị số nào để cho điều kiện (K) được thoả.
b) Xét trương hợp PG = 13 => 78 < MN < 91
Vì các số 1, 3 đã được sử dụng nên CDE có thể ở trong các khoảng (200,300), (300, 1000). (Nhớ rằng các số phải khác nhau và khác 0)
Để có CDE ở trong khoảng (200,300), ta phải nhân 13 cho số m > 15 và m < 24.
Với m trong khoảng đó, um > 100 , có 3 con số => không nhận được, trừ các trị số u = 6, 5, 4, 2
Xét trường hợp u/v = 6/13 và với m thay đổi trong khoảng (15,24)
Với m = 16 => vm = 13×16 = 208 => không nhận được vì chứa 0.
Với m = 17 => um = 6×17 = 102 > 100 => không nhận được và ngừng
Xét trường hợp u/v = 5/13 và với m thay đổi trong khoảng (15,24)
Với m = 16 => um = 5×16 = 80 => không nhận được vì chứa 0
Với m = 17 => vm = 13×17 = 221 => không nhận được vì có số 2 trùng nhau
Với m = 18 => um = 5×18 = 90 => không nhận được vì chứa 0
Với m = 19 => um = 5×19 = 95, vm = 13×19 = 247 => nhận được
Tóm lại: X = AB/CDE = 95/247 và Y = 86/13 là 1 đáp số của bài toán.
ĐỌC VUI VÀ SUY NGHĨ 
Kỳ BK085 « ĐỌC VUI VÀ SUY NGHĨ said
[…] đọc Chuyện Phiếm mới nhất: “Một bài toán mẫu tự đặc biệt”, trong mục Các Tài liệu mới […]